1. 講義の導入：動機とか今後の講義の構成とか
2. 物性物理としてのスピングラス
   • スピングラスの例
   • 実験的観測事実
   • スピングラス相のイメージ

大学院の講義には、大きく2つの特色があると思う。一つは、基本的なアドバンスな講義で(なんか日本語がヘン)、そこでは学部よりも難しいが基本的なことがらを学ぶ。場の理論とか、ここだとカオスとかだろうか。もう一つは、あるトピックを選んで、ちょっと専門色濃厚な講義かな。私は何を話そうかと悩んだ。手持ちの札がないので悩んだというのが主な理由だ。例えば、「相転移と臨界現象」とかやって、ループ計算ぐらいやってみようかとも思ったが、それならば別の人でもいいかとも思える。そこで、やはり?「ランダムスピン系の統計力学」をやることにした。(「計算機を使わないで計算物理手法」という企画もあったけど。。)
そんなマニアックな話しをする以上、説明責任があると強く思ったので、今日は、何故今(さら)スピングラスなのかをしゃべった(つもり)。 最近、情報統計力学なる言葉が一部で流行っている。何を隠そう私もその恩恵?をうけている。そこではレプリカ法とか平均場近似とかがリバイバルしているわけだが、その価値判断を冷静にできるためにも、そんな計算ができることは悪くないと考えたわけです。なので、この講義のゴールは、レプリカ法の計算ができるようになること、それからスピングラスの平均場理論でランダムネスをもつ統計力学模型について何がわかったかを明らかにすることです。

今日はまずは実験から入ろうと思ったので、スピングラス物質の例とスピングラス実験(必須事項?)を説明した。実験の話は、手で絵を書いて説明しようと思ったが、いかにも説得力がなかったので、今朝になって急遽、エジュメをつくった。しかし、論文からスクリーンショットで抜き出して、TeXに貼りつけたので、非常に絵が汚かった。申し訳ない。しかも、非線形帯磁率発散の図は以外とすぐに見付からずに、手持ちの紙をデジカメでとって、....とやったので、見るに耐えないものになってしまった。プロジェクター持っていって、移した方がよかったか。 次回は、モデルの話しからはじめたい。

1. RKKY相互作用を導出してみよう
   (2003.4.15) 答えを作ってみました。係数とか間違っているかも知れませんので、ご指摘下さい。。磁性の教科書には間違いなく解説されている事柄です。そして、スピングラスの教科書には間違いなく解説されていない事柄でもあります。明日の講義の準備を前に、またしても余計?なことをやってしまいました。ご参照下さい。PDF file(154KB)

1. 線形帯磁率のカスプって、どこが転移温度なのか?
   カスプを示す温度は交流帯磁率の周波数に依存します。ので、それをゼロに持っていった極限で行き着く温度がスピングラス転移温度になります。カスプができるのは、その周波数でスピンがついてこれなくなるためなので、本当に凍結相転移がおきているのであれば、無限にゆっくりと交流したときにもカスプると期待できます。自然な定義ですようね。ただし、実験で振れる交流帯磁率のレンジというのはそんなに広くないです。大体10^5くらいでしょうか。実際にはその範囲で凍結に見えるかどうかになります。
   微粒子磁性だと、相転移ではなくて、ブロッキングと言って、交流磁場についてこれないためにカスプを示すことがあります。この場合は周波数ゼロの極限は絶対零度になって、その意味でスピングラスとは区別されます。しかもその近付き方は熱活性化(exp(Δ/T))で決まっていて、活性化バリアエネルギーΔは微粒子の大きさで決まります。お配りした図の解像度が悪くて見にくかったですが、実はそれほどカスプ温度は動いていません。下の図を参照下さい。周波数が2.6Hzから1.33kHzと10^3程度変わっても、カスプ温度は、9.4Kから9.3K位(1%程度)しか変わっていません。 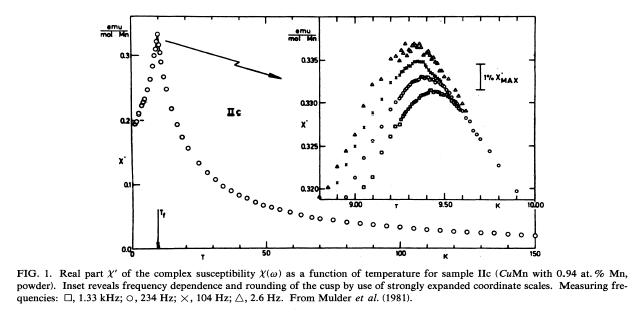まあ、これだけでは判断できないんですがね。もうちょっとやるとしたら、カスプ温度というのは、その温度での緩和時間が大体周波数の逆数位になったと解釈できるので、τ〜1/ω〜(T-Tg)^-zνというフッティングをやってT_gを見積もったりします。
2. 温度履歴って、どこが履歴なの？
   説明が悪かった。ZFCMは、Zero field cooled magnetizationです。ゼロ磁場で温度を下げて、ある温度で磁場をスイッチオンして、磁化を観測します。FCMは、Field cooled magnetizationです。磁場をスイッチオンしたまま、温度を下げながら、磁化を測定。これら2つは、温度を上ながら測る(ZFCM)と下げながら測る(FCM)がある温度を境に分岐して見えるということです。線形応答の範囲で見るので、m/hは磁場の大きさにはほとんど依存しません。また、FCMの方はよほどcooling (heating) rateが早くない限り、ほとんどリバーシブルです、つまり上げ下げ同じです。
3. 脇にある強磁性転移温度とスピングラス転移温度ってどのくらいちがうのか?
   こういうセンスすごいですね。どんなエネルギースケールでものが起こっているのかを抑えておくことはいつでも大事です。きっと常識的なんだと思うのですが、私が院生のころ(今もそうかな)は持っていなかったセンスです。これも、絵が悪かったんで、温度スケールがよくわからなかったですね。 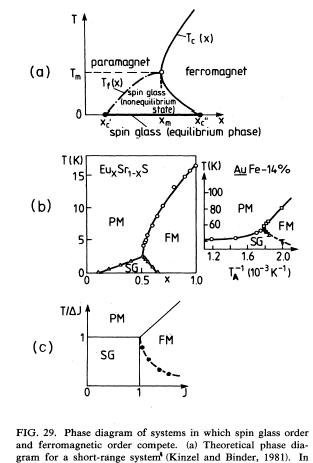真中の絵が、希釈したスピングラスの温度ー濃度相図です。大体一桁位下ルでしょうか？希釈系なので、磁性濃度が減るだけでエネルギースケールも下ルので、なんとも言えないところがありますが、メインのオーダが相互作用の競合のために消えて、次のスケールでスピングラスが見えるのだと思います。なので、一桁くらい下がります。
   FeMnTiO系のような濃い混晶系だと磁性イオンの濃度は変わりません。その場合だと両側の反強磁性転移が、大体60Kくらいなのに対して、真中のスピングラス転移は22Kなので、これは一桁まではいかないです。でもやっぱり、メインの相互作用よりはかなり低いところで転移します。
4. スピングラスのグラスは、ガラスと関係あるのか?
   なにか深遠な意味があるのか、とか、どこまでガラスを意識したネーミングなのかという質問だと思うが、まったくないと思う。どんな波数で展開しても、秩序が引っかからないので、周期性が全くないというところが、ガラスっぽいと言う程度だと思います。
5. まだ、他にもあったなー。

• 人前で話をするのはいつも緊張する。講義のたびにちょっとしたソウウツになってしまう。今日はそもそもどのくらいのひとがくるのかよくわからなかったという不安もあった。最終的には、20人位来てくれたであろうか？今度からちゃんとプリントすって来ます。さて、今日は特に初回だったので、緊張は倍増でした。加藤(雄介)さんから初回は大事だ、最初からビックリ箱を開けて見せないとダメだと忠告されていたので、その予定だった。が。。。。。今日は物性コテコテで一杯一杯だった。こんな話では次回は激減だろうなー。次の回はちょっと面白いかもよ、ここ読んでる人へ。
• ふと、私が受けた大学院の講義を思い出す。というか、私の場合は、講義の準備はどの方向の摂動にも不安定なので、こうした妄想も当然、レスポンス発散してしまう。大学の講義よりも、大学院の講義の方が印象に残っている。ただ単に時間がそれほど経っていないからかもしれない(ウソです。10年くらい経っています)。決して、内容を覚えているわけではないが、例えば、
  1. 宇川さんに素粒子理論(標準理論周辺)の講義(私は大学は筑波でした)。彼は、ノートは見ずにツラツラーと板書を続けて、ページをめくるためだけにノートに触れているようでした。すごい、このひとは全部頭の中に入っているんだと、Weinberg-Salamに感動するより、そっちに感動してました。本当の凄いのは短期記憶だったのかもってことはありません。
  2. 久保先生に相転移論。正直行って、ごった煮的な講義だった。しかし、そのどれもが結構今の知識になっているので、とても役にたった講義であった。熱力学極限の証明とか、Lee-Yang、Mermin-Wargnar、パイエルスの議論に高温展開。
  3. 高山先生にCDW
  4. 梁さんにCFT。「場の理論で大事なのは、regularizationだ」と言われたことくらいしか覚えていない。貴重な経験。
  5. 根本さんにスピングラス。この講義の元ネタです。
  6. 有光さんに「乱流」。その時に乱流勉強しながら、講義をしてくれたんだと思う。今や乱流で研究されています。もう一つ「dynamical symmetry breakingの例題としての超伝導」という講義も受けた。
  出来が悪かったんで、講義を受けたことしか覚えていないんですけどね。 これらの講義には及びませんが、また来週がんばります。