3. 運動方程式を解く
   1. 微分方程式の解法 つづき
   2. 放物運動
   3. 粘性抵抗のある落下運動

今日は一回目のレポートを返却することからはじまった．５分前くらいには教室についていたので，余裕のある人には講義の開始前に持っていってもらった．レポートについては，簡単なコメントをした．先週の反省から，このあたりで無駄な時間を費さないようにと思っていたのだが，結構余計なことをしゃべっていたような気がする．レポートはみなさんよく頑張っていたように思います．私なんかが気づかないような議論を展開していた学生もいました．レポート問題を考えることで，半ば強制的に足を止めてどっぷりと考えることができれば，それでよいと思います．というより，大学一年二年というのは，忙しいようでも，たっぷりと時間がある時期なんだと今の私には思えます．演習書の問題をやって，ある特定の解法を身につけたり，マスターすることも大事かもしれませんが，問題解答マシーンなどではなくて，じっくり考えることにも取り組んでほしいものです．

といつjも心の中で考えているものの，ここ前回の後半と今回だけは，完全に解法伝授の講義になっています．まあ，問題を解けないと始まらないですからね．今回は定数係数の二階微分方程式の特性方程式による解法の話をしました．あーして，こーして，そーすると，これが一般解になります．こんな説明では到底納得いかねーぞー，というのは極めて健全です．納得行かないところが明確になったら，是非かかってきてほしいと思います．こちらからは，いくつかの捕捉をしておきました．おそらく，一番の疑問は「それで解になっているのか?」という疑問だと思いますが，それは直接微分方程式に代入してみれば，解になっていることはわかります．それはやってみればわかりますし，また，初期条件の指定をすれば他に解はないことは示すことが出来ます．証明はA4二ページくらいか．

これで二通りの解き方を示したので，応用を考えて行こう．2つは適用範囲は違うのでその点は注意が必要である．まず最初の例は放物運動であるが，これは以前に一度解いたことがあったので，そのまとめをした．２次元空間での運動はいつでも放物運動になることがわかる．ここで休憩の替わりとして，レポート問題2の解説をしてみる(どうもレポートはネタのようになっているな)． 次に，空気抵抗を考慮にいれた落下運動を考えてみる．まずは，運動方程式を書き下す．先ほどの鉛直方向の運動方程式に，速度に比例した抵抗力が働く場合を問題にする．もしも最初から質点だと考えれば，空気抵抗をどのように考えればよいかわからなくなってしまう．実際に前回のレポートのなかに，質点ではまずい例として，それが上げられていた．確かにまずいと考えるのは間違いではない．しかし，例えばブーメランの例でもそうであるが，運動の説明という観点から，ブーメランに働いているだろう力を推測して運動方程式を考えてみることは悪いことでない．運動方程式を右から見るか，左からみるかの違いがあるという典型例ではないかと思ったので，このタイミングでもう一度質点についての議論をしてみた．

ここでタイムアップ．最後に解くべき微分方程式をまとめてみると，今日の前半示した定数係数二階線形微分方程式(非斉次版)になっていることがわかる．そこで，「ステップ１：なんとか特解を１つみつけてくる」が早速問題になっている．睨めば見えて来る．やってみよう．来週はここから始まる．

練習問題2の解答例とレポート問題2です．

今日は小道具はなし．本当になし．

1. 放物運動のグラフを書いてみよう．
2. 放物運動の最高到達点と，そのときの時刻を求めよう．
3. 空気抵抗があるときの微分方程式を解いてみろ．

レポート問題の１一番，角度θが図と文章で大小関係がちがう．

あれ，反対でした．困惑させたようで申し訳なかった．どっちでもよいので，解答に分るように書いてください．

特解って，どこの解?

求めたい微分方程式の解です．こんな解答でよかったっけか．

オーダーΔtって何のこと．

Δtのべき級数展開したときの，Δt程度の大きさ(Δtの高次の微小量を含む)を表している．これは一度説明した方がいいですね．

一般解がそうなるのはどうして?法則?

これが一番多い疑問．上のような解答ではだめでしょうか． 初期条件付きで唯一であることを示せば納得します?

• 今日の出席者数は，77でした．止まりましたー!!投票用紙になぜか「仮面ライダー」さんがいましたが，しっかり人数に数えました．ここまで減ったので，これから増えるというのは厳しいでしょうね．この数が最終回までもつようにがんばりたいところです．
• 全然関係ない話ですが，私が通った筑波大学には当時，一学喫茶という喫茶店が構内にありました．食券制で，食券の裏に自分の名前を書くことなっていまして，料理が出来たときに，喫茶店のおねえさんがその名前を呼んでくれるのですが，それがどんな名前でも気持ちよいくらいに豪快に呼んでくれます．「クリームソーダーを御注文の仮面ライダーさーん」．洒落のわかるおねえさんでした．上の仮面ライダーをみて，ふと思い出しました．
• 今日は遅ればせながら，第一回レポートを返しました．レポートにも感想を書いてもらっていたので，その返答もここに載せてもよかったかもしれません．しかし，残念ながら，メモを取る前に返却してしまったので，載せられません．個別には赤(正確にはピンクペン)で返答しておきました．そうそう，全部で96本のレポートを見ましたが，今日の出席者は77．是非，なんとかして受け取ってください．私の部屋の前のポストに入れておきます．切角の赤が無駄にならないように．
• レポートを返却できたので，遠慮なく?次のレポート問題を出しました． 牛乳ケースを持ち上げる給食当番問題とサッカーボール蹴っ飛ばし問題と空中で止まって見える問題を出しました．しかし，みなさんはもう給食の牛乳は瓶ではない世代のようで，重いケースを二人で運んだよね?っていうことには同調してもらえなかった．最近，おじさんになってきたと感じることが多くなってきたが，またひとつ淋しい事実を認識してしまった．それから３番はあんまりこちらから情報を出さないように，詳しい説明はしませんでした．難しい問題ですが，頑張って考えてくれれば幸いです．質問があったら，メールでも掲示板でも結構ですよ．というかね，掲示板作ったんだけど，利用されなくてね．自分で書くか?
• 今日のコメントより

ぶつぶつぶつぶつ．

えーい，うるさい!

微分方程式がイマイチよくわからないので，適度な問題ください．

来週配ります．

２階線形微分方程式のステップ2で，どうして突然y=e^λxとおいたのですか?

どうして突然y=e^λxとおいたのの?

同感．突然のeの出現にとまどってます．

ウム．ワシもじゃ．

この質問が二枚の投票用紙に同時に発生しました．(今反省しても仕方がないかも知れませんが，指数関数はOKだったでしょうか?)質問はこうでしょうか．それでよいのは続くステップから理解したが，そもそもじゃ，なーぜにそうおいたのじゃ．y=x^λではだめなのか?
それは指数関数が線形微分方程式と相性がいいからです．一階の線形微分方程式というのは，ある関数yについて，微分したらものが元の関数に比例している方程式です．あるいは二階だと，二階微分まで含めて，元の関数で表せる方程式です．一方で，指数関数というのも，微分をとると元の関数に比例しています．x^λはそうでありませんし，指数関数以外にはありません．ここに指数関数に置く理由があります．どうでしょうか．

レポートは鉛筆でなく，ペン書の方がよかったですか?

いいえ，そんなことはありません．

両面刷のプリントで表と浦が上下になっています．いつも，向きを揃えて欲しいです．

今日コピー取ってるときに気づいたんだけど，もう間に合わなかった．

ハタチになってからロクなことがない．

シチなことは?

問題を解いて慣れる方が個人的には良い気がするのですが，何か演習書でもやった方が良いのですか?

やらないよりはやった方がいいのでしょうね．でも，演習書をやることで，満足してしまっては，上の方に書いた問題があると思います．問題を解けることは必要条件ですが，解けるようになることが理解の全てではけっしてありません．私もできるでけ，練習問題を配るようにがんばります．

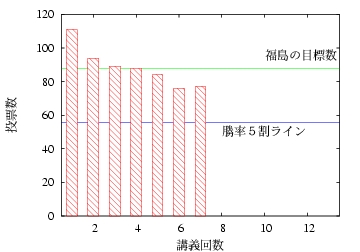
出席率5割切り?

おいおい，そんなこと言うなよー．

髮切った?

はい．

コメントが限りなくゆるい気がする．

先週のこのページ読みましたか?私もそう思っています．もっとも，私もゆるいコメント返していますけど．．．その後にでも，真剣な議論が始まることもあろうかと．．．

• 今回は更新が遅れちゃった．