5. 振り子からぶらんこへ
   1. たちこぎ つづき
6. 運動する座標系と慣性力
   1. ガリレイ変換と慣性力(お話)
   2. 回転座標系と慣性力

前回に立ち漕ぎの運動方程式を書き下しておいたので，今日はその典型的なパラメータのときの答えを紹介しました．ちゃんとしめすのはそれなりに面倒くさいですが，共鳴が起こるw=2w0の場合はアウトラインを示しておきました．興味のある人は実際に解く過程をたのしんでみて下さい．この立ち漕ぎの方程式は，Mathieu(マチウ)方程式呼ばれている有名な微分方程式で，パラメーター共鳴という共鳴を起こす典型的な方程式です．他にも同様にパラメータ共鳴を起こす方程式はたくさんあります．線形微分方程式の中にも面白い挙動をしめすものがいろいろあるようです．さて，共鳴の仕方について，いくつか強制振動の共鳴と比較しならがまとめておきました．こんな感じ．

さて，ここで一息いれる．金曜クラスでは，どうして今回のシリーズでブランコを取り上げたかの理由を話した．それは昨年もやったということもあるが，それよりも５月の連休に見た遊園地の乗物によるところが大きかった．芸人としては?，同じネタでつなぐのもどうかと思い，今日は新ネタを持ってきた(そういうネタでなくて，講義のネタを考えろよな，というツッコミはある)．それは，「念じれば振れるコイン」である．名付けて「バッファローズ１号」．ちょっと写真じゃ見にくいかも知れないけど，実物を見た人にはわかるでしょう．ヨタ話は下に．．．

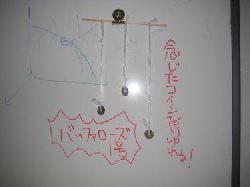
おもしろ実験系の本には必ず乗っているおもちゃだけど，せっかく微分方程式で振り子を解いたので，前の晩にこそこそとつくって来た．原理は詳しく説明しなかったけど，わかっただろうか．なぜ念じたコインだけが振れるのかということは，わからなくても自分では出来ることが多い．「ほら，こうすればできるだろう」と小学生には「説明」できる．中学生にはどうかなー．「実はこれはぶらんこを漕ぐことと一緒だよ」と説明するか．高校大学生にはそれではダメで，やはり運動方程式を解いて示したい．「これが共鳴だ」とね．それから，どうして念じていないコインは振れないのかということも，ここまでくれば「分かる」．運動方程式を解いただけではピンとこないことも，こうした実物を見ればまたもう一歩分かった気になるし，実はもう一歩先に行けば最先端の研究まで行けるのではないかと言う気もする．
共鳴現象は身の回りにたくさんある．例えば，電子レンジもある意味で共鳴だし(実はちょっと難しい)．講義では思いついたものを説明したが，「よい」ことばかりしか話さなかった．世の中には起こって欲しくない共鳴もある．例えば，壊れそうな部品がさらなる振動によって，共鳴的に壊れてしまうとか，首都高にのると，道路が揺れていたりするが，橋の固有振動で共鳴なんか起こってしまうと，崩壊してしまう．工学としては，共鳴が起きないように制御することが大事であったりするようである．

さて，残った時間で，運動座標系の話しへ入る．特にここでは回転する座標系に現れる見かけの力について考察したい．講義の３回目くらいの時に，ガリレイ変換と慣性力の話しはした．慣性力の例は，電車が曲がるときや走り出したりするときに感じる，謎の力である．遠心力やコリオリ力も同種の慣性力であり，それらを今から導出しようというわけである．回転座標を導入して，考え方のアウトラインを示した後に，こしこしと時間微分をはじめる．止まっている方での運動方程式を使うと，慣性力が出て来る．すでにここでコリオリ力と遠心力が出てきたが，来週は改めてこの辺りから話しを進める．

1. Mathieu方程式解いてみる?

式変形ヘン

幾つか板書のミスを指摘してもらいました．最後に「確かコリオリ力はどっちかマイナスのはず」という指摘には驚きました．感覚として，そういうことを覚えているのならば素晴しいです．

O(h²)って何?展開?

以前にも出てきたような疑問ですが，ゆっくり説明しました．あんな感じでわかったでしょうか?これは数学なんですが，数学者はしない変形かもしれません．何か小さなパラメータ(今の問題だとぶらんこの立ち漕ぎ幅h)について，0の近傍での(テーラー)展開します．hが小さければその近似はよいわけですが，どのような意味で「よい」かといえば，指標がO(オーダー)です．おおざっぱに言えば，その時の精度を表しています．O(h²)とはh²程度の大きさの項のことです．最初のころにプリントで配ったと思いますが，sin xをxが小さいと思って，「展開」したときにO(x)までの近似やO(x²)までの近似ではどの程度あっているかをグラフに描いてあります．いろんな関数について，自分で確かめてみるといいでしょう．

ところで相対論では．．．

とはじまる疑問を受けました．ちゃんと答えていたかどうかは不明です．ブルーバックスを読んでもった疑問だそうです．一度ちゃんとした専門書を読んでみるのがいいと思います．

今日のコメントから

ビリヤードしたい

そーか，やりたいのか．

今週は勉強強化週間です．図書館で閉館まで勉強しています． 物理もいままでサボっていた分を一気に復習するつもりです．

頑張って下さい． 最近ちょくちょく図書館にいったりします．新しくてきれいな図書館ですね．図書の量はそれほど多いとは思いませんが，机はたくさんあって，勉強するには良いところだと思います．私は学生のころはあんまり勉強しませんでしたが，図書館の記憶はよく覚えています．人生のうちにこれほど図書に囲まれることはないでしょう．今のうちに是非堪能して下さい．

立ちこぎは自励振動じゃないのですか?

違います．自励振動というのは，振動的でない一方行的な外力から自立的に振動が出て来る現象で，バイオリンを弦で引くときには，弦を一方行にしか引かないが，弦は振動するので音が出てきます．他には．．．ところが，立ち漕ぎの場合は人間(重心位置)の振動運動をうまく共鳴条件に合うように揺らすことによって，振り子の振動を揺らします．ちょっと違いますね．立ち漕ぎは，パラメタ−励振と呼ばれています．パラメータ励振を示す微分方程式系は他にもいろいろあるようです．

• 今日の参加人数は，70.また微妙に減ったなー．もうちょっとだがんばってくれー!
  
• (上から) 前の晩にこっそりとつくったのが，このバッファローズ一号(きっと改良されるはず)である．何度も練習して，わかったことは，少々別のコインが振れてもあわてないことである．前回配ったプリントにあるグラフを思い出してみると，共鳴振動からずれた振り子も全く振れないわけではなくて，途中で位相がずれていることからちゃんと減衰するわけである．確かに，じっとがまんして揺らしていると，お望みのコインだけの振幅が大きくなる．さて，朝起きて，子供に実験してみる．寝ているところを叩き起こしたのが，すべての失敗の元だったかもしれない．しかし，とにかく，実験は成功．途中でとなりのコインが振れ出したところで，「エエエーイ」と改めて念を送ってみるという演出は練習の時からの計算済み．うまくいくと素直に驚くのは子供のよいところである．ここからは物理学から児童心理学の世界に突入する．子供は誰でも自分でやってみたくなるものだろう．それは共通だろうが，どのようにするかは子供に依存する．うちの子はいきなり念をおくりはじめた，「バッファローズ1号」は私がもったままで．それでは．．．やはりいじわるして，私は何もしない．．．ちゃんと揺らしてやって，不思議さを大きくしてやるのがよかったかもしれないが，ここは「父親の威厳」を植え付けようというやましい心を優先させたわけである．結果は，寝起きの不機嫌さもあいまって，「バッファローズ1号」破壊という暴挙にでよった．やっぱ寝起きはこわいのである．そうこうしているうちに妻が拾いあげて，コインをゆらしはじめた．「父親の威厳」は崩壊し，意地悪な父親像だけが残った全くブルーな朝になってしまった．
• まったくどうでもよい話だが，今週の一番ショックなニュースは「近鉄合併問題」であった．あんな弱小球団なくなってもだれも困らないというのが一般的な意見かもしれないが，ファンはそうはいかないだろう．コインのおもちゃの名前の由来は，近鉄の名を忘れないようにということである．話せば長いが，私は子供のころからの近鉄ファンである．パ・リーグはテレビ中継などないので，ラジオによくかじりついていた．どうしてファンになったかというと，その勝ちっぷりがいつも感動的であったからである．それに12球団の歴史の中で唯一日本一になっていないという事実も応援したくなる要因かもしれない．もっとも日本一に近付いた瞬間はおそらく「江夏の21球」のときだったのだろう．日本シリーズだけはテレビでもやっていたので，脳裏に映像つきで覚えている(山際氏の「江夏の21球」が後に記憶を補間しているのかもしれない)．あのシリーズの江夏は結構打ち込んでいて，あの9回のノーアウト満塁の場面で負けはないと思っただけに，悔しい思いをしたものである．最後のバッターは石渡であった．その石渡は今では二軍の監督になり，先日ウエスタンリーグの優勝を決めた．一軍は合併が決まった後の話だっただけにちょっと寂しくなってしまった．なんとかがんばって，今年最後のチャンスに日本一になってもらいたいものである．全然物理とは関係ないお話でした．
• なんだか，全然反省していないなー．そういうわけではないですよ．